Relative entropy, also known as Kullback-Leibler divergence, is a measure of the asymmetry of the difference between the two probability distributions P and Q. Recently, CMU’s Assistant Professor Simon DeDeo stated on Twitter: “The fields in which KL divergence is used are very extensive, including psychology, epistemology, thermodynamics, statistics, computation, geometry, etc. This topic I can open a seminar."
So, Simon Dedeo listed on his Twitter the use of KL divergence in various fields, and attached related articles. Zhizhi organizes and compiles as follows:
psychology
In the field of psychology, KL divergence can be used as an excellent predictor of where attention is directed. In a paper published in the University of Southern California in 2005, researchers used data streams and novel mathematical methods to explore the brain's response in a surprising situation. They believe that surprise is a general, theoretical concept that can be generated by first principles and can also be formed by the spatial and temporal dimensions, the sensational patterns and data types, and data sources.
Using Bayesian framework theory, the researchers capture the prior probability distribution of the experimental object and then express the background information as:
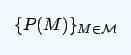
The model or hypothesis is M. With the prior distribution, the basic impact of the new data D is to convert the prior distribution to a posterior distribution {P(M|D)}, expressed as:

In this framework, if the subject's emotions are not affected, then D does not contain surprise emotions, that is, posterior and a priori are the same. On the other hand, if the subject produces surprising emotions, then posterior and prior will produce distance. So researchers measured the distance between the posterior and a priori indirectly to measure whether there was surprise or not. This uses the KL divergence and is expressed as:

Paper address:ilab.usc.edu/surprise/
Cognitive
The KL divergence can be used as a measure of the direction of the experiment (maximizing the effect of the model). In general, T-optimality is used to obtain an optimal design to resolve homoscedastic models with a normal distribution. This function has been extended to also study heteroscedasticity and binary response models in literature. In a 2007 paper, researchers from Spain and Italy proposed a new standard based on the KL distance to distinguish the corresponding models without dynamic distribution.
statistics
The application of KL divergence in statistics may be too much, but the author focuses on its failure as a tool to measure the approximate solution. In the author's blog, there was such an example: Suppose we are space scientists and we come to a distant strange planet. We want to study a kind of insect on the planet. The bug has 10 teeth, but after a long life, the teeth of the insects. Some of the samples were removed. After collecting some of the samples, we obtained the following number distribution of teeth:
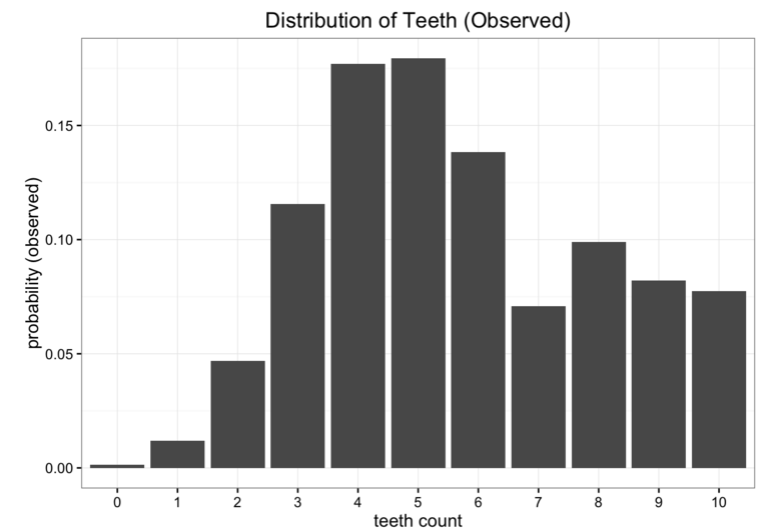
Although the data is good, there is a slight problem. We are too far away from the Earth and the cost of transferring data back is too high. We now want to simplify the data into a simple model, leaving only one or two parameters. One of the methods is to represent the number of teeth of a bug in a uniformly distributed manner. We know that there are 11 possible situations in total:
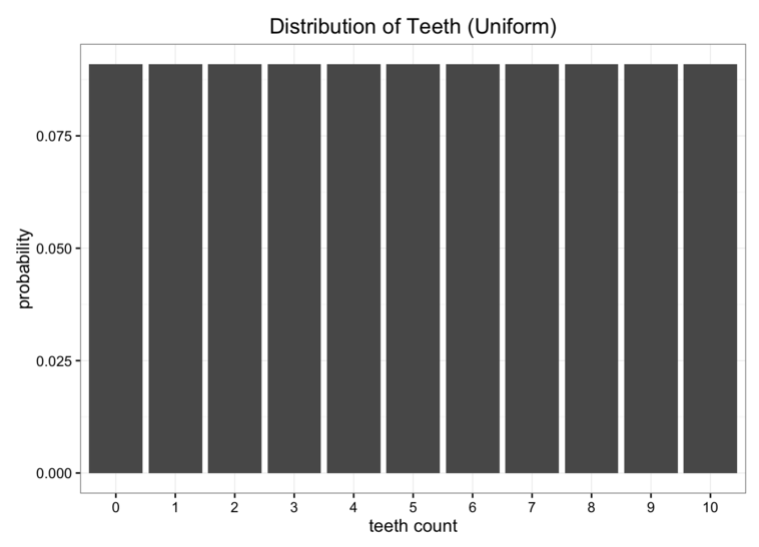
Obviously, our data is not evenly distributed, but it does not look like some of the distribution patterns we normally see. Another way is that we can try to model the data with a binomial distribution. In this case, what we need to do is estimate the probability parameters in the binomial distribution. We know that if the number of trials is n and the probability is p, then the expected value is E[x]=nâ‹…p. In this case, n=10, the expected value is the average number of our data, and the hypothesis is 5.7. So our best estimate of p is 0.57. The resulting binomial distribution is as follows:
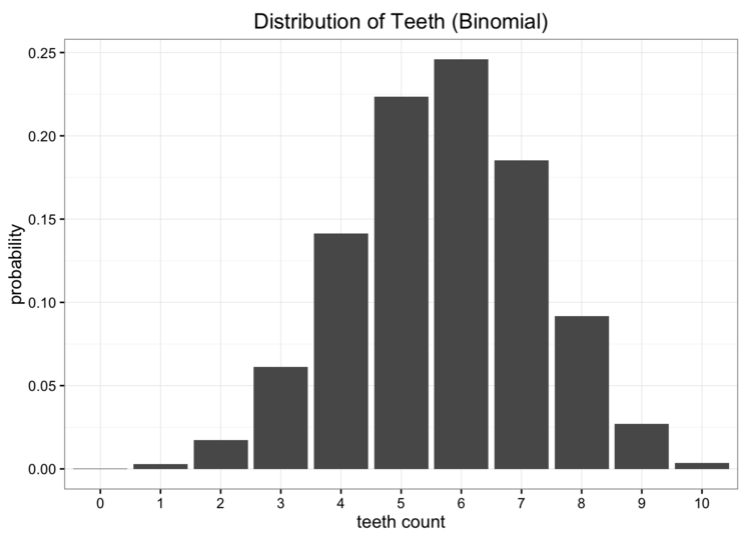
Comparing these models with the original data, none of them fit perfectly, but which one is better?
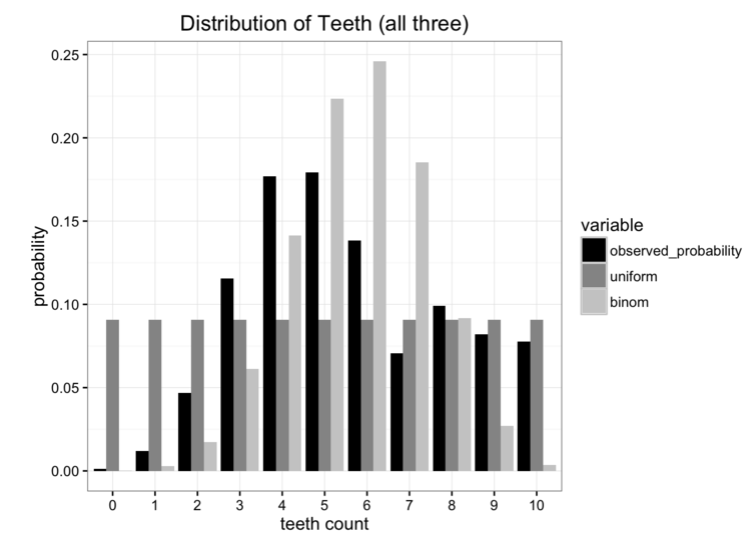
Although there are some wrong indicators, our initial goal is to minimize the amount of information sent. So, the best way to know that the model retains the most raw data is to use KL divergence.
Calculation (machine learning)
The KL divergence can be used as a tool for detecting whether the model is valid or not, that is, it can display the useless information of the model. In a paper published by Still et al. in 2012, they used KL divergence to test the quality of the model.

Another machine learning application: KL divergence (usually called "cross-entropy" in this case) is used as a basic loss function for automatic encoders, deep learning, and so on.
In addition, it can also be used as algorithmic fairness. How to limit a predictive algorithm in the best way while also ensuring fairness. The author of this article and published a paper in 2016 to study the variables in big data.
The author believes that when we use machine learning to handle public policy, we find that many useful variables are combined with other problematic variables. This phenomenon is even more serious in the era of big data. Some predictions do not have strong theoretical support at all. If high-quality algorithms do not provide strong proof, making arbitrary decisions is very dangerous. In order to ensure the accuracy of the prediction, the author used KL divergence to compare the two decisions.
Thesis address: arxiv.org/abs/1412.4643
Calculation (compression)
When a compression algorithm designed for a system cannot be applied to another system, it is necessary to use KL divergence for calculation.
Cultural development
We believe that KL divergence can also be used as a measurement standard for individuals to develop and innovate. In a 2016 paper, researchers believe that research in unfamiliar environments with uncertain resource distribution will always fluctuate between new and old discoveries, and the two must be balanced. In the process of finding information, it is also true that those who are thirsty for knowledge will always hesitate to study in a known field or develop new fields of research. In order to study this decision process, they used Darwin as an example to find out all the books that appeared in his reading notes and used KL divergence to generate a model that quantified his reading choices.
Thesis address:S0010027716302840
At the same time, KL divergence can also be used to study the creation of competition and cooperation and the sharing of ideas. In a paper published shortly before, American researchers used KL divergence to study how people made democratic decisions during the French Revolution.
Paper address:
Quantum theory
University of Cambridge student Felix Leditzky wrote a doctoral dissertation on the introduction of relative entropy and its application in quantum theory, including how KL divergence generates quantum in the case of interchange operators. The paper consists of 200 pages. Interested students can read it.
Paper address: pdfs.semanticscholar.org/30a7/6a44a4f0f882c58bd0b636d6393956258c3f.pdf
User @postquantum added: "If you have some limited categories of operations, then KL divergence will tell you how much raw material you need (research results, quantum entanglement, information), this measurement is unique." Specific reference papers: Arxiv.org/abs/quant-ph/0207177
Also if you want to use generalized entropy and hyperstatistics (ie coupling systems), this is a special case of Rényi entropy.
Paper address:
Digital Humanities
KL divergence is related to TFIDF, but when it comes to coarse graining, KL divergence performs better. (The most prominent words have a higher KL when sorting files; stop words have the lowest KL). Specific can see related papers.
Paper address:
economics
In addition, KL divergence also appeared in economics. Twitter users @itsaguytalking published papers and used KL divergence to study the trade between different countries. The purpose of the paper's research was how to measure the distance between different opinions.
Paper Address: ~ez2197/HowToMeasureDisagreement.pdf
biology
In a 2015 paper, the researcher Nihat Ay believes that the interdependent type of random interaction units is usually derived from the KL of the static joint probability distribution, and the probability distribution comes from the corresponding parameter set. The settings in this paper extend from static to dynamic, using Markov chain information geometry to capture temporary interdependencies.
Paper address:
geometry
When the differential geometry is extended to a probability simplex, KL divergence is used as a non-measurement connection.
Thermodynamics
A measurement method that can be extracted from an unbalanced system to make it balanced.
Conclusion
Thus, KL divergence is one of the concepts of probability and has been applied in many fields. In addition to the fields described above, the most commonly used field of KL divergence is statistics. In addition to the usefulness mentioned above, it is also the basic criterion for the Akaike information criterion in terms of model selection.
Insulated Copper Tube Terminals
Insulated Copper Tube Terminals,High quality insulated terminal,copper tube terminal
Taixing Longyi Terminals Co.,Ltd. , https://www.lycopperterminals.com